曾彪彪的个人博客 -- 马拦过河卒

# P1002 [NOIP 2002 普及组] 过河卒

## 题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。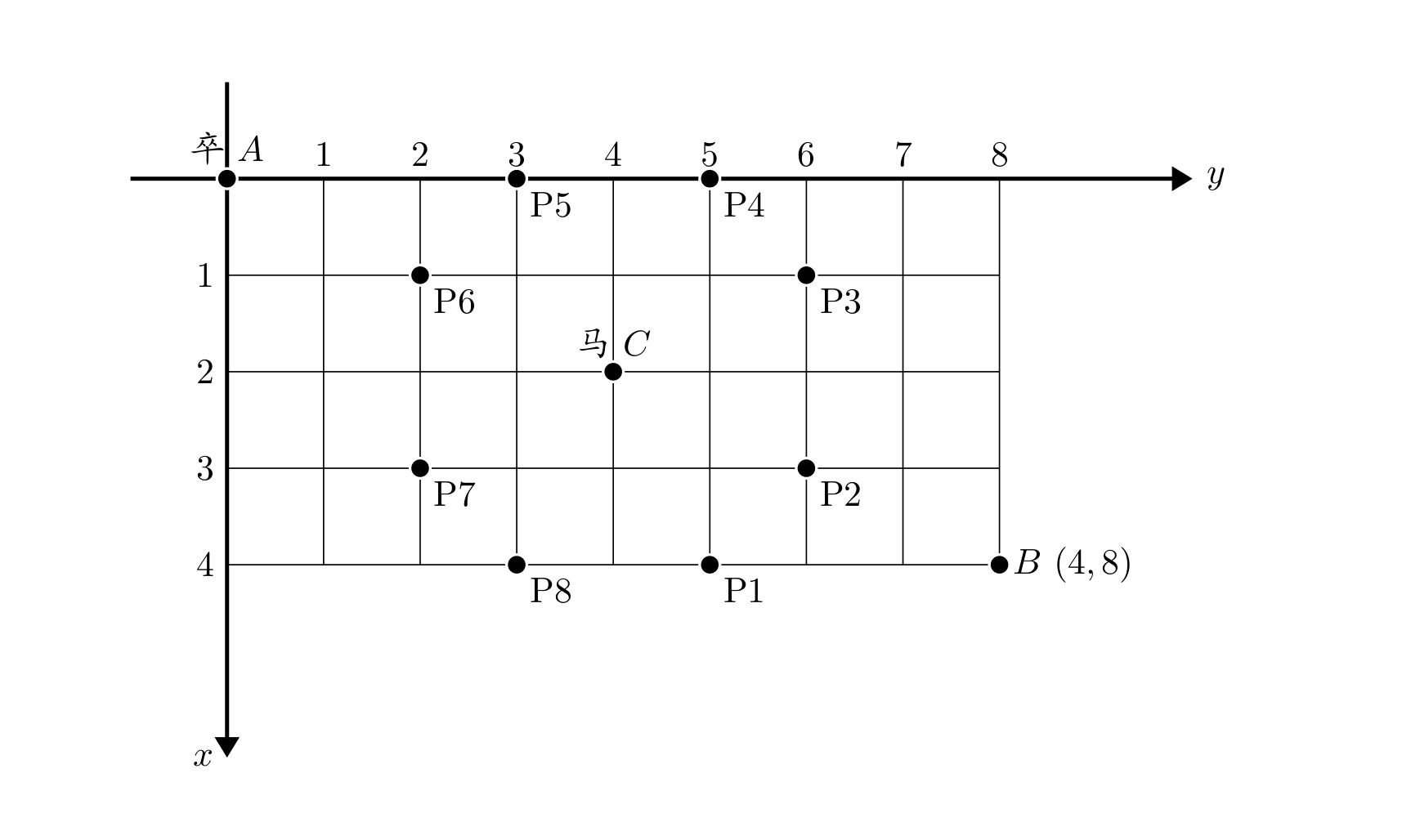

![](https://cdn.luogu.com.cn/upload/image_hosting/ipmwl52i.png)

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

## 输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

## 输出格式

一个整数，表示所有的路径条数。

## 输入输出样例 #1

### 输入 #1

```
6 6 3 3
```

### 输出 #1

```
6
```

## 说明/提示

对于 $100 \%$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

**【题目来源】**

NOIP 2002 普及组第四题

---

这题刚开始使用递归来实现，只能得60分，因为递归太深，会爆栈。代码如下：
```c++
/**
start time: 8:45
End time:
Type: simulator
Solution:
list all location can't be reached
dfs(x,y)
-
-
-
test case:
-
-
-
-
first submit score: 100
cause:

**/

#include <bits/stdc++.h>
using namespace std;

int bx, by, cx, cy;
vector<vector<bool>> grid(25, vector<bool>(25, false));
int ans = 0;

void dfs(int x, int y)
{
    if (x == bx && y == by)
    {
        ans++;
        return;
    }
    if (x > bx || y > by)
    {
        return;
    }
    if (grid[x][y])
    {
        return;
    }
    dfs(x + 1, y);
    dfs(x, y + 1);
}

int main()
{

// freopen("C:/Users/zengsam/Downloads/P1042_2.in", "r", stdin);

cin >> bx >> by >> cx >> cy;
    vector<int> dx = {2, 2, -2, -2, 1, 1, -1, -1};
    vector<int> dy = {1, -1, 1, -1, 2, -2, 2, -2};
    for (int i = 0; i < 8; i++)
    {
        int lx = cx + dx[i];
        int ly = cy + dy[i];
        if (lx >= 0 && ly >= 0)
        {
            grid[lx][ly] = true;
        }
    }
    grid[cx][cy] = true;

if (grid[0][0] || grid[bx][by])
    {
        cout << 0;
        return 0;
    }

dfs(0, 0);
    cout << ans;

return 0;
}

```

后来想到了动态规划，之前学过一点点，正好能用到。代码如下：
```c++
/**
start time: 8:45
End time:
Type: simulator
Solution:
list all location can't be reached
dfs(x,y)
-
-
-
test case:
-
-
-
-
first submit score: 100
cause:

**/

#include <bits/stdc++.h>
using namespace std;

int bx, by, cx, cy;
vector<vector<bool>> grid(25, vector<bool>(25, false));
vector<vector<long long>> dp(25, vector<long long>(25, 0));

int main()
{

// freopen("C:/Users/zengsam/Downloads/P1042_2.in", "r", stdin);

cin >> bx >> by >> cx >> cy;
    bx += 2;
    by += 2;
    cx += 2;
    cy += 2;
    vector<int> dx = {0, 2, 2, -2, -2, 1, 1, -1, -1};
    vector<int> dy = {0, 1, -1, 1, -1, 2, -2, 2, -2};
    for (int i = 0; i < 9; i++)
    {
        int x = cx + dx[i];
        int y = cy + dy[i];
        grid[x][y] = true;
    }

dp[2][1] = 1;

for (int i = 2; i <= bx; i++)
    {
        for (int j = 2; j <= by; j++)
        {
            if (grid[i][j])
            {
                dp[i][j] = 0;
            }
            else
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }

cout << dp[bx][by];

return 0;
}

```

后来看一位大佬写的代码，动态规划还能优化，将dp由二维改成一维，代码如下：

```c++
/**
start time: 8:45
End time:
Type: simulator
Solution:
list all location can't be reached
dfs(x,y)
-
-
-
test case:
-
-
-
-
first submit score: 100
cause:

**/

#include <bits/stdc++.h>
using namespace std;

int bx, by, cx, cy;
vector<vector<bool>> grid(25, vector<bool>(25, false));
vector<long long> dp(25, 0);

int main()
{

// freopen("C:/Users/zengsam/Downloads/P1042_2.in", "r", stdin);

dp[2] = 1;

for (int i = 2; i <= bx; i++)
    {
        for (int j = 2; j <= by; j++)
        {
            if (grid[i][j])
            {
                dp[j] = 0;
            }
            else
            {
                dp[j] = dp[j - 1] + dp[j];
            }
        }
    }

cout << dp[by];

return 0;
}

```

这里的一维数组dp，存储了到目前为止，可能的路径。在dp[j]未计算之前，dp[j]存储的是i-1行时的路径，如果计算d[j]+=d[j-1]，那么就是计算当前行i，对应的可能路径。

马拦过河卒 - 动态规划入门

评论(0)